Análisis de Regresión

En este tutorial, vamos a utilizar un conjunto de datos de la muestra obtenida de 20 vendedores diferentes. El modelo de regresión trata de explicar y predecir las ventas semanales de un vendedor (variable dependiente) utilizando dos variables explicativas: Inteligencia (IQ) y la extroversión.

Proceso

En primer lugar, vamos a organizar nuestros datos de entrada. Aunque no es necesario, se acostumbra a colocar todas las variables independientes (X 's) a la izquierda, donde cada columna representa una variable única. En la columna más a la derecha, colocamos la respuesta o los valores de las variables dependientes.

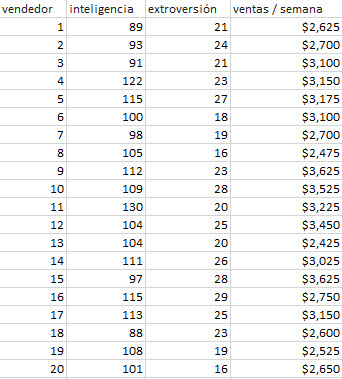
En este ejemplo, tenemos 20 observaciones y dos variables independientes (explicativas). La cantidad de ventas semanales es la respuesta o variable dependiente.

Ahora estamos listos para llevar a cabo el análisis de regresión. En primer lugar, seleccione una celda vacía de la hoja de cálculo en la que desea que la salida sea generada, a continuación, busque y haga clic en el icono de regresión en la pestaña NumXL (o barra de herramientas)

Ahora aparecerá el wizard o asistente de regresión.

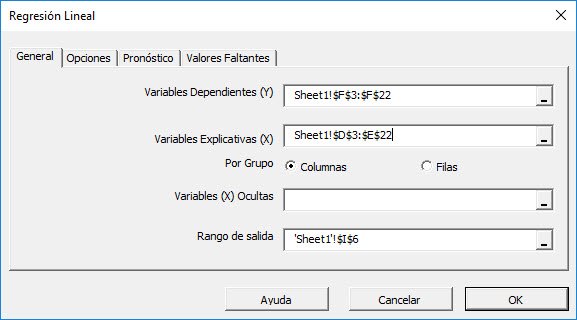
Seleccione el rango de celdas para los valores variables de respuesta/dependiente (es decir.ventas semanales). Seleccione el rango de celdas para los valores de las variables explicativas (independientes).

Finalmente, una vez seleccionemos el rango de celdas X y Y, las pestañas "opciones," "pronóstico" y "valores faltantes" comenzaran a estar disponibles (habilitadas).

Next, select the “Options” tab.

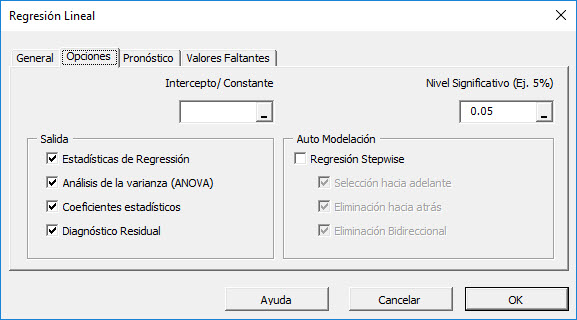
Inicialmente, la tabulación se fija para los siguientes valores:

• La intercepción, constante de regresión se deja en blanco. Esto indica que el intercepro de regresión va a ser estimado por la regresión. Para fijar la regresión a un valor fijo (por ejemplo. cero(0)), ingreselo aquí.
• El nivel de significancia (aka.) se fija a 5%.
• En la sección de salida, se selecciona el análisis de regresión más común.
• Para auto-modelado, vamos a dejarlo sin marcar. Vamos a discutir esta funcionalidad en una edición posterior.

Ahora, de clic sobre la tabulación o pestaña "Valores Faltantes".

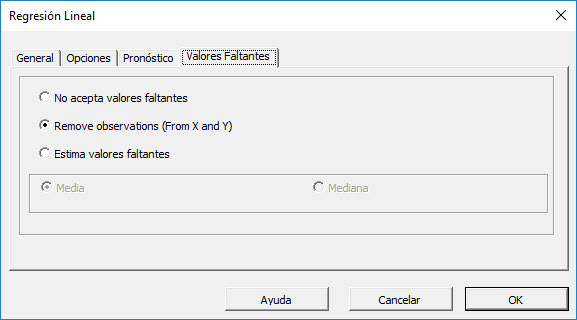
En esta tabulación, usted puede seleccionar puede seleccionar el método para manejar los valores que faltan en el conjunto de datos (X y Y). Por defecto, cualquier valor que falta se encuentra en X o en Y de ninguna observación excluiría la observación del análisis.

Este tratamiento es un buen enfoque para nuestro análisis, así que vamos a dejarlo sin cambios.

Salida

Ahora, haga clic en "OK" para generar las tablas de salida.

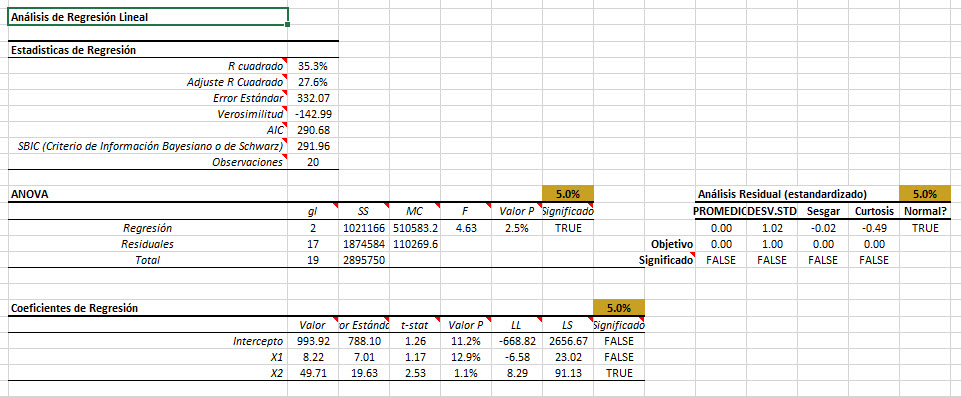
Análisis

Examinemos ahora las diferentes tablas de salida más de cerca.

1. Estadísticas de la regresión

En esta tabla, se muestra una serie de estadísticas de resumen de la bondad del ajuste del modelo de regresión, dada la muestra.

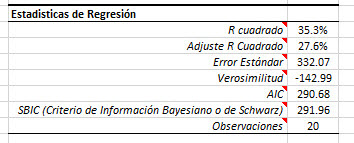
1. El coeficiente de determinación (R cuadrado) describe la relación de la variación en Y descrita por la regresión.
2. El ajuste R - cuadrado es una lteración de R cuadrado para tomar en cuenta entre el número de variables explicativas.
3. El error estándar es el error de regresión. En otras palabras, el error en el pronóstico tiene una desviación estándar alrededor de $ 332.
4. Función de log-verosimilitud (LLF), criterio de información Akaike (AIC) y criterio de información Bayesiano/Schwartz (SBIC) son diferentes medidas probabilísticas para la bondad de ajuste.
5. Por último, "Observaciones" es el número de observaciones faltantes no utilizados en el análisis.

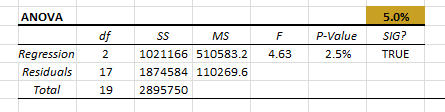
2. ANOVA

Antes de que podemos considerar seriamente el modelo de regresión, debemos responder la siguiente pregunta:

"Es el modelo de regresión estadísticamente significativo o una anomalía de datos estadística?"

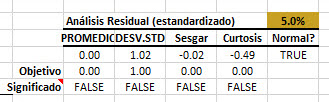
3. Tabla de diagnóstico de residuos

Una vez que confirmamos que el modelo de regresión explica algunas de las variaciones en los valores de la variable de respuesta (ventas semanales), podemos examinar los residuos para asegurarse de que se cumplan los supuestos del modelo subyacente.

4. Coeficientes de la tabla de regresión

Una vez que se establece que el modelo de regresión es significativo, podemos mirar más de cerca a los coeficientes de regresión.

Cada coeficiente (incluyendo el intercepto) se muestra en una fila separada, y calculamos las siguientes estadísticas:

• Valor (i.e. \alpha,\beta)
• Error estándar en el valor del coeficiente.
• Puntaje de la prueba (T-stat) para las siguientes hipótesis:
  H_o: \beta_k = 0
  H_1: \beta_k \neq 0
• Los valores de P de la prueba estadística (utilizando la distribución t de Student)
• Límites superior e inferior del intervalo de confianza para el valor del coeficiente.
• Una decisión de rechazar/aceptar para la significancia del valor del coeficiente.

En nuestro ejemplo, sólo la variable "extroversión" se considera significativa mientras que el intercepto y la "Inteligencia" no se consideran significativas.

Conclusión

En este ejemplo, encontramos que el modelo de regresión es estadísticamente significativo para explicar la variación en los valores de la variable de ventas semanal, esta satisface las suposiciones del modelo, pero el valor de uno o más coeficientes de regresión no es significativamente diferente de cero.

¿Qué hacemos ahora?

Puede haber una serie de razones por las que este es el caso, incluyendo la posible multicolinealidad entre las variables o simplemente que una variable no debe ser incluida en el modelo. A medida que aumenta el número de variables explicativas, responder a esa pregunta es más complicado y necesitamos un análisis más profundo.

Cubriremos este tema particular en una entrada aparte de nuestra serie.

Tutorial Video